
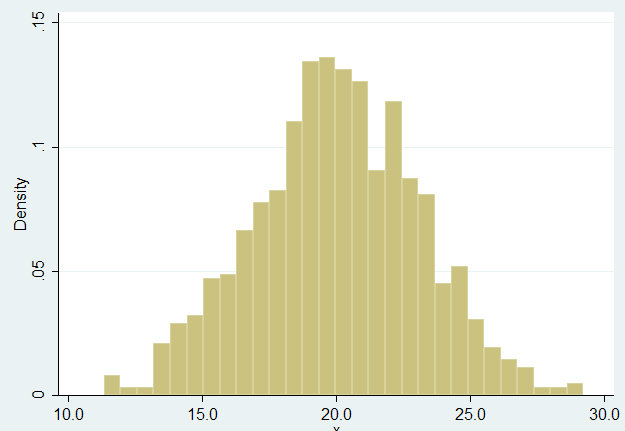
Any empty cells or cells containing non-numeric data are ignored.įor Example 1, we see that JARQUE(A4:A23) = 1.93 and JBTEST(A4:A23) =. If pop = TRUE (default), the population version of the test is used otherwise the sample version of the test is used. JBTEST(R1, pop) = p-value of the Jarque-Barre test on the data in R1 JARQUE(R1, pop) = the Jarque-Barre test statistic JB for the data in the range R1 Real Statistics Functions: The Real Statistics Resource Pack contains the following functions. 05, once again we conclude there isn’t sufficient evidence to rule out the data coming from a normal population. The JB test can also be calculated using the SKEWP (or SKEW.P) and KURTP functions to obtain the population values of skewness and kurtosis.

05, based on the JB test, we conclude there isn’t sufficient evidence to rule out the data coming from a normal population. Observation: Related to the above properties is the Jarque-Barre (JB) test for normality which tests the null hypothesis that data from a sample of size n with skewness skew and kurtosis kurtīased on using the functions SKEW and KURT to calculate the sample skewness and kurtosis values. Both statistics are within two standard errors, which suggests that the data is likely to be relatively normally distributed. 55 (cell D16) the standard error for the kurtosis is 1.10 (cell D17). Similarly, if the absolute value of the kurtosis for the data is more than twice the standard error this is also an indication that the data are not normal.Įxample 1: Use the skewness and kurtosis statistics to gain more evidence as to whether the data in Example 1 of Graphical Tests for Normality and Symmetry is normally distributed.Īs we can see from Figure 4 of Graphical Tests for Normality and Symmetry (cells D13 and D14), the skewness for the data in Example 1 is. If the absolute value of the skewness for the data is more than twice the standard error this indicates that the data are not symmetric, and therefore not normal.

incomeprepared.dta for a file from a parent directory Stata only opens a dataset if the data in memory are unchanged from. dta can be opened with the use command: Æ Syntax: use filename.dta Æ Example: use incomeprepared.dta or: use. The three lines of the program do the following: A Brief Introduction To Stata With 50+ Basic Commands 8/28 use Datasets with the Stata specific ending.
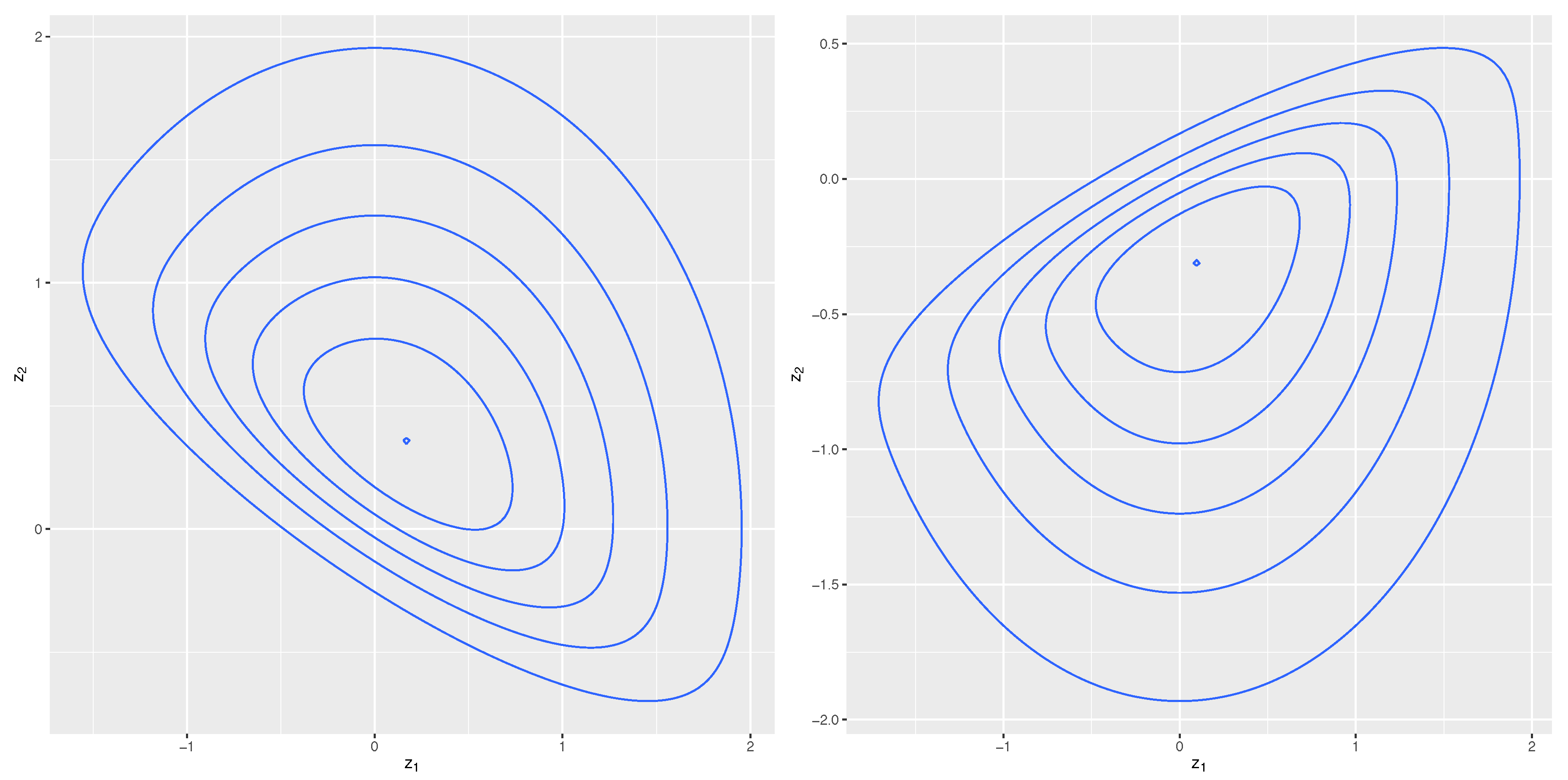
We need the program to calculate the correlation, extract the value from r(rho), calculate the Fisher- \(z\) transformation, and return that value to r(). This makes the usual formula for a confidence interval, \(r \pm t_ \right) Without a transformation, the correlation coefficient is bounded in the interval \(\). We would like to also calculate the confidence interval for the correlation. The sample correlation coefficient between LSAT and GPA is 0.776. We want to estimate the correlation between LSAT and GPA scores. We have 15 paired observations of student LSAT scores and GPAs. The data used in this tutorial are from Efron and Tibshirani’s (1993) text on bootstrapping (page 19). See our blog post on bootstrapping for more specifics on the formulas used for the different types of bootstrap confidence intervals.
#Stata 13 skew how to
This tutorial demonstrates how to use bootstrapping to calculate confidence intervals in Stata. The bootstrap is most commonly used to estimate confidence intervals. You can calculate a statistic of interest on each of the bootstrap samples and use these estimates to approximate the distribution of the statistic. The bootstrap is a statistical procedure that resamples a dataset (with replacement) to create many simulated samples.


 0 kommentar(er)
0 kommentar(er)
